
Figure 1: An illustration of the three particle system.
Outcomes: (i) This work extends the three-particle Calogoro model by allowing the particles to have different charges; (ii) This extended model provides information on the relative stability of two and three particle complexes in one-dimensional quantum wires; (iii) New analytically approximate solutions to the Heun differential equation were found and a new trigonometric identity extending an identity by Calogora was identified.
This web page is structured as follows:
Imagine a one-dimensional (1D) system containing three electrons restrained to move within a segment by harmonic potentials. In classical mechanics a harmonic potential may represent a spring. Consider a point along the 1D axis and denote this point the origin. Attach three springs to the origin and the other ends of the springs to each of the three electrons. This 1D system may be visualised as follows:
Electrons expel each other by the Coulomb interaction. Hence, the model in Fig. 1 would be very predictable (and boring) if no springs were present; since the electrons would just expel each other until separated by an infinite distance. However, by including the springs we have a much more interesting situation where electrons try to expel each other and the springs try to force the electrons towards a center point (the origin).
The "physics" motivation for studying this model is linked to nano-structure devices; an example is a so-called quantum-dot device trapping a single electron.
Although the model in Fig. 1 may look simple the quantum mechanical equation for this model cannot be solved analytically. However, Calogoro [1] showed that, using a modified Coulomb potential an analytical solution can be found - the corresponding model is today known as the Calogoro model [1].
The Coulomb potential between two electrons decays as one over the distance between the electrons; an effect of this is that the further the electrons are apart the weaker the repulsion between them. The modification Calogoro made was to say: assume that the potential between two electrons decay as one over the squared distance between the electrons. Mathematically, this modified Coulomb potential can be written as
where x1 and x2 are the position coordinates of electron 1 and 2. In comparison the Coulomb potential has the form
We took on the challenge of extending the work of Calogoro [1] by allowing one of the three electrons to be a 'hole'; a 'hole' is semiconductor speak and models a positively charged electron. Studying this system took place in two stages.
1. Doing the mathematics. Showed [2] that solving the Schrodinger equation for the two-electron-one-hole system can be reduced to the problem of solving a Heun differential equation. Heun's equation is fairly well studied in the literature [3], although cases for which analytical solutions to this equation are known are rare. However, through further considerations, I found analytically approximate solutions accurate for the regions of physical interest, and in this process the following trigonometric formula:
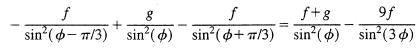
which for the special case f = -g reduces to the trigonomtric identity found by Calogero [1]. Denote qee to be the strength of the interaction between two electrons and qeh the strength of the interaction between a hole and an electron, then it was observed that the potential energy of the Hean differential equation can be approximated highly accurately as shown in the figure below
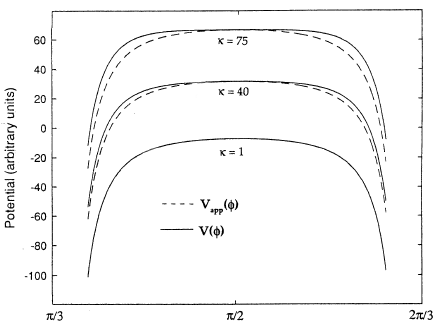
The ratio kappa = qee / qeh measure the relative strength of the electron-electron interaction and electron-hole interaction. The dotted lines shows the approximate potential, and even for a value of kappa = 40 the approximate potential is very close to the exact potential and for kappa <= 1 they are visually indistinguishable. For typical practical electronic devices kappa is expected to be less than 10. Within this approximation Heun's equation transforms into the problem of solving a hypergeometric equation for which known analytical solutions exist.
2. Interpretation of the analytical solutions. Use the following notation:
Which of these complexes are most stable for different values of the electron-electron interaction strength qee and electron-hole strength qeh? To investigate this the 'interaction' energy, Eint, for the two complexes are compared; where 'interaction' here refers to the energy difference between the total energy of a complex with the interaction between the particles turned off (by setting qee, qeh = 0) and not turned off. The interaction energy for the two complexes are
for the X complex, where
and
for the X- complex. A closer analysis of these expressions reveals that if the ratio qee / qeh is less than 11, then X- is more stable than X measured in terms of interaction energy. Therefore if this ratio is less than 11, as is the case for typical experimental devices, this would suggest that X- is more strongly bound than X.