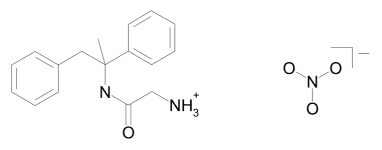
Figure 1: The structures of the remacemide ion to the left and nitrate ion to the right.
Outcome: Applying the maximum likelihood method in the context of structure solution from powder diffraction data.
This web page is structured as follows:
The maximum likelihood method is perhaps one of the oldest and most used methods in applied statistics. This method aims to calculate the probability, p(data| params), of some data being true given a set of parameters of a model are true. Finding the maximum likelihood then correspond to locating the set of parameters that maximises the likelihood probability. This set of parameters is often referred to as the maximum likelihood estimate.
Prior to this work the maximum likelihood had been successfully applied to the study of single-crystal data, in particular in the field of macromolecular crystallography, see for example [1-5]. To purpose of this work was to carry the success of applying the maximum likelihood method over to the analysis of powder diffraction data. A powder diffraction pattern can be viewed as a 1D projection of a 3D single-crystal pattern and as a consequence of this, peaks well separated in the single-crystal pattern may overlap in the powder pattern. In [6] we formulated a likelihood figure-of-merit, FOM-LIKE, suitable for powder diffraction that can be calculated almost as fast as the standard least-squared figure-of-merit (FOM-LS). The FOM-LS includes the assumption that the model used to fit the data is flawless. This assumption is relaxed in the design of the FOM-LIKE figure of merit, where parts of the model can be associated with uncertainty.
As an example, consider determining the crystal structure of remacemide nitrate by first locating the larger remacemide ion and thereafter the position of the smaller nitrate ion; the latter task is trivial, once the remacemide ions is correctly located. The remacemide ion and nitrate ion are shown in the figure below.

First the FOM-LS is used to locate the remacemide ion. That is, the nitrate ion is treated as non-existent. The result of this is demonstrated in Fig. 2, which compares the correct crystal structure of remacemide nitrate on the left with the best structure obtained using the FOM-LS (for more details see [6])
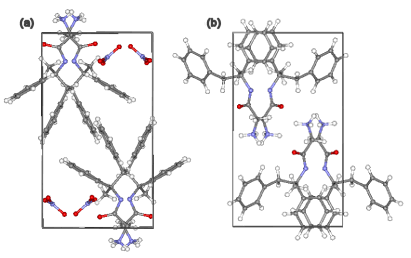
Using FOM-LS implicitly assumes that the incomplete model (consisting of the remacemide ion only) is the complete model, an effect of this is that the remacemide ion is twisted, such as to try to occupy both the space meant for this ion and the nitrate ion; the result is that the remacemide ion ends up 'somewhere in between' the nitrate ion and remacemide ion as seen by comparing Fig. 2(a) and Fig. 2(b).
Using the FOM-LIKE it is possible to improve this situation. The FOM-LIKE allows parts of the model to be earmarked as being highly uncertain, more specifically, allows some of the positional coordinates of the model to be treated as completely uncertain. Repeating the simulation in Fig. 2 using the FOM-LIKE the result in Fig. 3 is obtained. Here, the positional coordinates of the nitrate ion are treated as completely uncertain. That way, we recognize the 'presence' of the nitrate ion, although with its position coordinates treated as completely uncertain, and this is an improvement compared to treating the nitrate ion as 100% non-existent. This improvement is seen by comparing Fig. 2 and 3; in Fig. 3 the correct motif of the remacemide ion is revealed unlike in Fig. 2.

In summary, the maximum likelihood approach presented here allows for parts of the model to be treated as highly uncertain. Such a treatment might be advantageous in a structure solution approach when parts of the model are suspected to be disordered, or if it is desirable to reduce the complexity of the structure solution task by initially only solving for parts of the model.