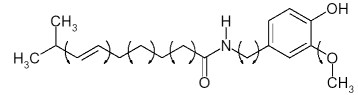
Figure 1: The molecular structure of capsaicin. The arrows denote torsion angles that cannot be assigned correctly in advance of a structure determination.
Outcome: Introduction of existing computer search algorithm into the field of structure determination from powder diffraction data.
This web page is structured as follows:
The hybrid Monte Carlo (HMC) global optimisation algorithm presented here has its origin in numerical simulations in lattice field theory. It is a method that aims to combine key components of molecular dynamics and the Monte Carlo approach into one efficient algorithm for exploring a search space.
Here the position and orientation of molecular fragments and internal torsion angles within fragments make up the search space. These 'degrees of freedom' (DOF) can be varied and the collection of all possible DOF configurations defines the search space. A figure-of-merit (FOM) function is associated with the search space, that is, for each configuration a FOM value can be calculated. In solving a crystal structure, the goal is to search for the configuration that matches the lowest possible value of the FOM function; this configuration is the global minimum of the FOM.
The HMC algorithm [1] takes the following approach. Imagine a fictive particle whose coordinates are defined by the DOF of the search space. Further, interpret the FOM function as the potential energy function of this fictive particle. Then imagine 'kicking' this particle and observing the path it follows according to the classical (Hamiltonian) equation of motions – this is the molecular dynamics component of the algorithm. The Monte Carlo component is included to 'patch' a known problem of molecular dynamics. Due to numerical rounding errors it is computationally difficult to maintain the fictive particle on the (correct) path as dictated by the Hamiltonian equation of motions, and the particle tends to 'drift' off this path. To reduce the 'damage' of this effect, at appropriate intervals the particle is 'stopped' and an assessment is made (using a Metropolis criterion) whether the particle has moved too far of its path – this is the Monte Carlo component of the algorithm; if the particle has drifted too far it is returned to its previous position. Regardless of whether the particle is returned to its previous position the particle is 'kicked' off in a new direction in the search space.
A number of different search algorithms have been applied for structure determination from powder diffraction. One of the more frequently used is simulated annealing (SA), for instance used in the commercial software DASH. To judge the efficiency of the HMC algorithm presented here it was compared with the simulated annealing algorithm in the DASH software via the structure solution of Capsaicin, see the figure below.

The bond angles and bond length between atoms in the Capsaicin molecule can be looked up in a crystallographic database, for instance using the CSD (Cambridge Structural Database). The 9 'torsion' angles, indicated by the arrows in Fig. 1, are unknown. For a given conformation of these torsions angles and a given position and orientation of the molecule in the unit cell (another 6 degrees of freedom) a dataset can be calculated. This calculated dataset can then be compared to the observed dataset by means of a FOM. The smaller the FOM the better the fit is between the calculated and observed dataset, and the structure which corresponds to the smallest value of the FOM is most likely to correspond to the actual crystal structure.
The crystal structure of Capsaicin was searched for in twenty independent attempts using the HMC algorithm and twenty independent attempts using the SA algorithm. The results obtained using the HMC algorithm are illustrated in the figure below.
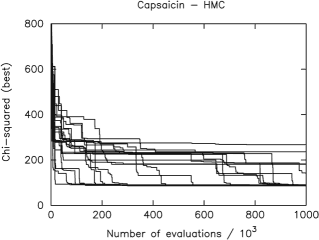
The speed of the algorithm is proportional to the number of times the FOM function is evaluated. The fewer such evaluations are used to reach the configuration corresponding to the global minimum of the FOM, the faster the algorithm. In Fig. 2 the smallest FOM value recorded after a given number of evaluations is displayed for twenty independent HMC runs. The global minimum of the Capsaicin FOM is just below 90, from Fig. 2 it is seen that 15 of the 20 runs the HMC algorithm successfully reached this target. The equivalent plot using the SA algorithm is shown in Fig. 3.
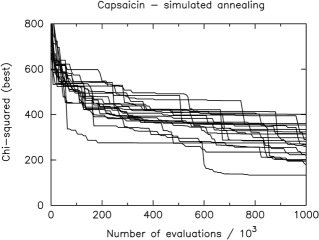
The SA algorithm was successful in only 1 out of 20 runs. Thus, the efficiency of the HMC algorithm is clearly demonstrated.
The first version of this document was completed 8/10-04.